Today, we implement a program based on reinforcement learning that uses Bellman Q-learning technique. The technique is based on updating a table of values, assigned to each action in each state. The target in each state is to find the action that maximizes the accumulated future values.
In our code, we consider an N-by-N environment, with a Target cell and Pitfall cell who end the game. Each movement has a small cost. So the algorithm is supposed to learn how to reach the target from any point of the grid through the shortest path. I also explain the impact of future reward discount factor, learning rate, and exploring to exploiting ratios.
The code is available on my Github
# www.soligale.com
# Reinforcement learning, Bellman Q learning value function
import numpy as np
import matplotlib.pylab as plt
grid_size = 10
n_actions = 4 # 0, 1, 2, 3 => Left, Right, Up, Down
target = (7,7)
pitfall = (5,3)
rewards = np.full((grid_size, grid_size), -2)
rewards[target] = 100 # Goal state
rewards[pitfall] = -100 # Pitfall state
rewards[(7,6)] = 2
rewardsarray([[ -2, -2, -2, -2, -2, -2, -2, -2, -2, -2],
[ -2, -2, -2, -2, -2, -2, -2, -2, -2, -2],
[ -2, -2, -2, -2, -2, -2, -2, -2, -2, -2],
[ -2, -2, -2, -2, -2, -2, -2, -2, -2, -2],
[ -2, -2, -2, -2, -2, -2, -2, -2, -2, -2],
[ -2, -2, -2, -100, -2, -2, -2, -2, -2, -2],
[ -2, -2, -2, -2, -2, -2, -2, -2, -2, -2],
[ -2, -2, -2, -2, -2, -2, 2, 100, -2, -2],
[ -2, -2, -2, -2, -2, -2, -2, -2, -2, -2],
[ -2, -2, -2, -2, -2, -2, -2, -2, -2, -2]])Q_table = np.zeros((grid_size, grid_size, n_actions))
epsilon = 0.01 # Randome action
alpha = 0.4 # Learning rate
gamma = 0.98 # Discount factor for future rewards
def choose_action(Q_table, state, epsilon):
if np.random.uniform(0, 1) < epsilon:
return np.random.randint(0, n_actions)
else:
return np.argmax(Q_table[state])cumulative_rewards = []
episode_lengths = []
for episode in range(500):
state = (np.random.randint(0, grid_size), np.random.randint(0, grid_size))
done = False
total_reward = 0
steps = 0
while not done:
steps += 1
reward = 0
action = int(choose_action(Q_table, state, epsilon))
if action == 0: # Left
if state[1]%grid_size != 0:
next_state = (state[0], state[1] - 1)
elif state[0] > 0:
next_state = (state[0] - 1, grid_size - 1)
else:
next_state = (grid_size - 1, grid_size - 1)
elif action == 1: # Right
if state[1]%grid_size != grid_size - 1:
next_state = (state[0], state[1] + 1)
elif state[0] < grid_size - 1:
next_state = (state[0] + 1, 0)
else:
next_state = (0, 0)
elif action == 2 and state[0] > 0: # Up
next_state = (state[0] - 1, state[1])
elif action == 3 and state[0] < grid_size - 1: # Down
next_state = (state[0] + 1, state[1])
else: # blocked on the top or bottom borders
next_state = state
reward = rewards[next_state]
total_reward += reward
# Update Q-value using Bellman equation
Q_table[state + (int(action),)] = Q_table[state + (int(action),)] + alpha * (reward + gamma * np.max(Q_table[next_state]) - Q_table[state + (int(action),)])
state = next_state
if next_state == target or next_state == pitfall or steps > 200:
done = True
episode_lengths.append(steps)
cumulative_rewards.append(total_reward)
Q_table[target] = [0, 0, 0, 0]
Q_table[pitfall] = [0, 0, 0, 0]
plt.plot(cumulative_rewards)
plt.title("Cumulative reward vs Episode")
plt.show()
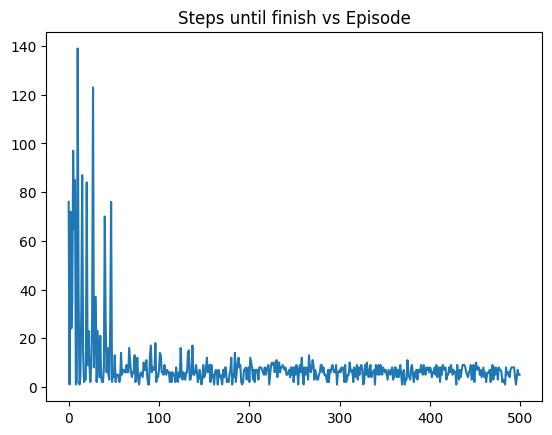
plt.plot(episode_lengths)
plt.title("Steps until finish vs Episode")
plt.show()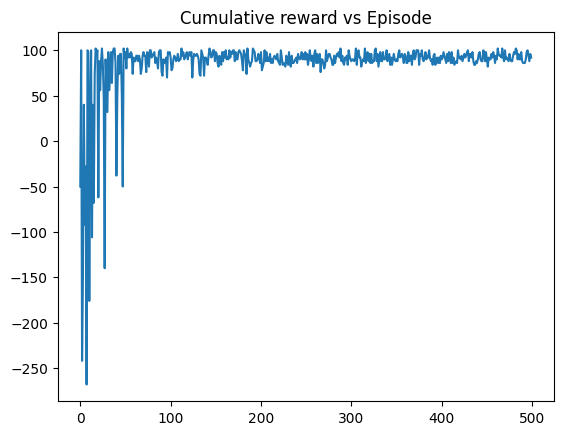
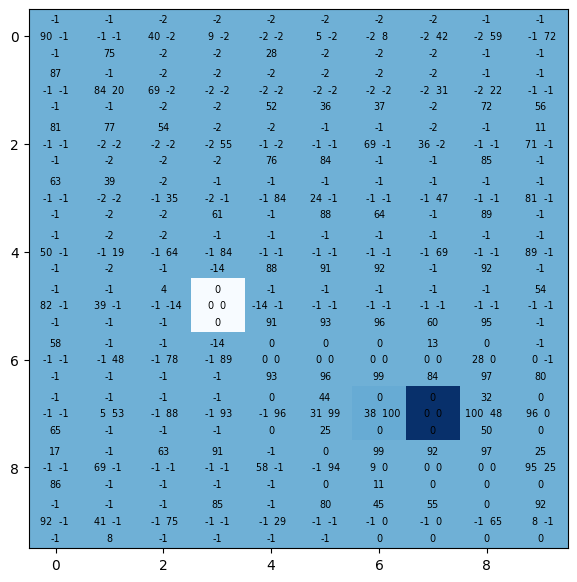
Q_table2 = Q_table / Q_table.max() * 100
plt.figure(figsize=(7,7))
plt.imshow(rewards, cmap="Blues")
# LRUD
for j in range(grid_size):
for i in range(grid_size):
plt.text(j,i,f"{round(Q_table2[(i, j, 0)])} ", ha="right", va="center", size="x-small")
plt.text(j,i,f" {round(Q_table2[(i, j, 1)])}", ha="left", va="center", size="x-small")
plt.text(j,i,f"{round(Q_table2[(i, j, 2)])}\n", ha="center", va="bottom", size="x-small")
plt.text(j,i,f"\n{round(Q_table2[(i, j, 3)])}", ha="center", va="top", size="x-small")
plt.show()